扩散模型DDPM
结构:级联去噪模型
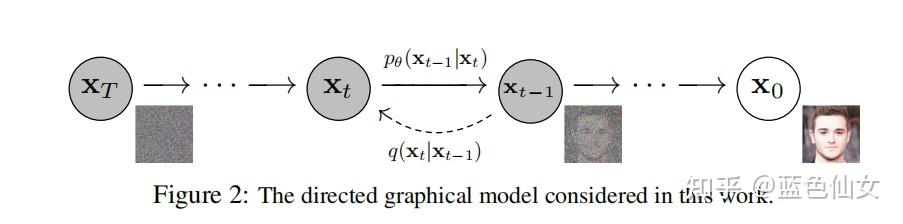
前提
1.任何一张图像
(Batch Size, Channels, Height, Width)
Batch Size (B):一批处理多少张图片。在训练时通常大于1(如16, 32),在生成单张图时为1。
Channels (C):颜色通道。
- 对于彩色图(RGB),Channels = 3。
- 对于灰度图,Channels = 1。
Height (H):图像的高度(像素数)。
Width (W):图像的宽度(像素数)。
2.1)
2.2)
步骤:
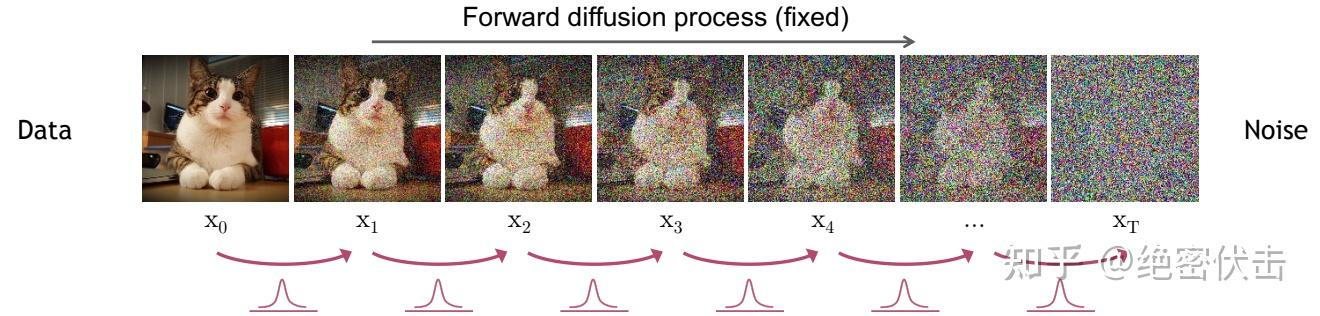
一.前向过程
前向扩散:前向过程是加噪的过程,前向过程中图像 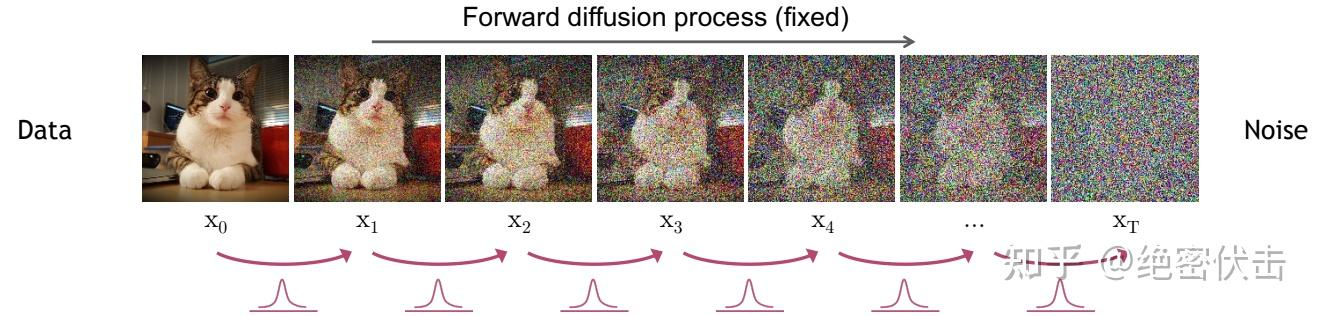
微观:
宏观:
前向过程的图像
eg.一维高斯分布函数 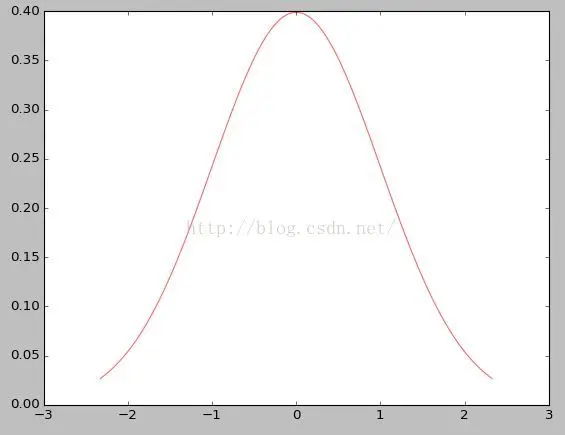 二维高斯分布函数
二维高斯分布函数 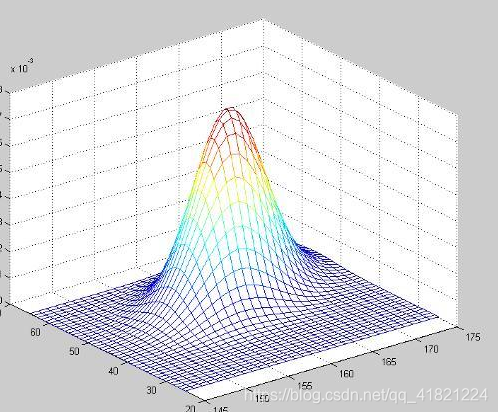 多维...
多维...
二.逆向过程
反向去噪:DDPM使用神经网络拟合逆向过程,因为实际的去噪过程的噪声是未知的,想要得到好的去噪的效果,要先投喂数据,然神经网络记住这些样例噪声的特征,让后去噪的时候神经网络就可以预测一个和前向过程在相似的噪声,并达成生成类似照片的效果。如果得到好的逆向过程就可以通过随机噪声,逐步还原出一张图像。
宏观:
我们的目标是找出
因为由于不知道
又因为一个高斯分布
按
一旦我们完成了第三步,我们就得到了
准备完成了以后外面要开始考虑我们不知道
但是这里面又得到未知数,即噪声
但是这得到了原理怎么训练吗?算出
attention: 1.无论是前向过程还是反向过程都是一个参数化的马尔可夫链(Markov chain),其中反向过程可用于生成数据样本(它的作用类似GAN中的生成器,只不过GAN生成器会有维度变化,而DDPM的反向过程没有维度变化)
训练
DDPM 论文中通过神经网络(通常是 U-Net)拟合噪声预测模型 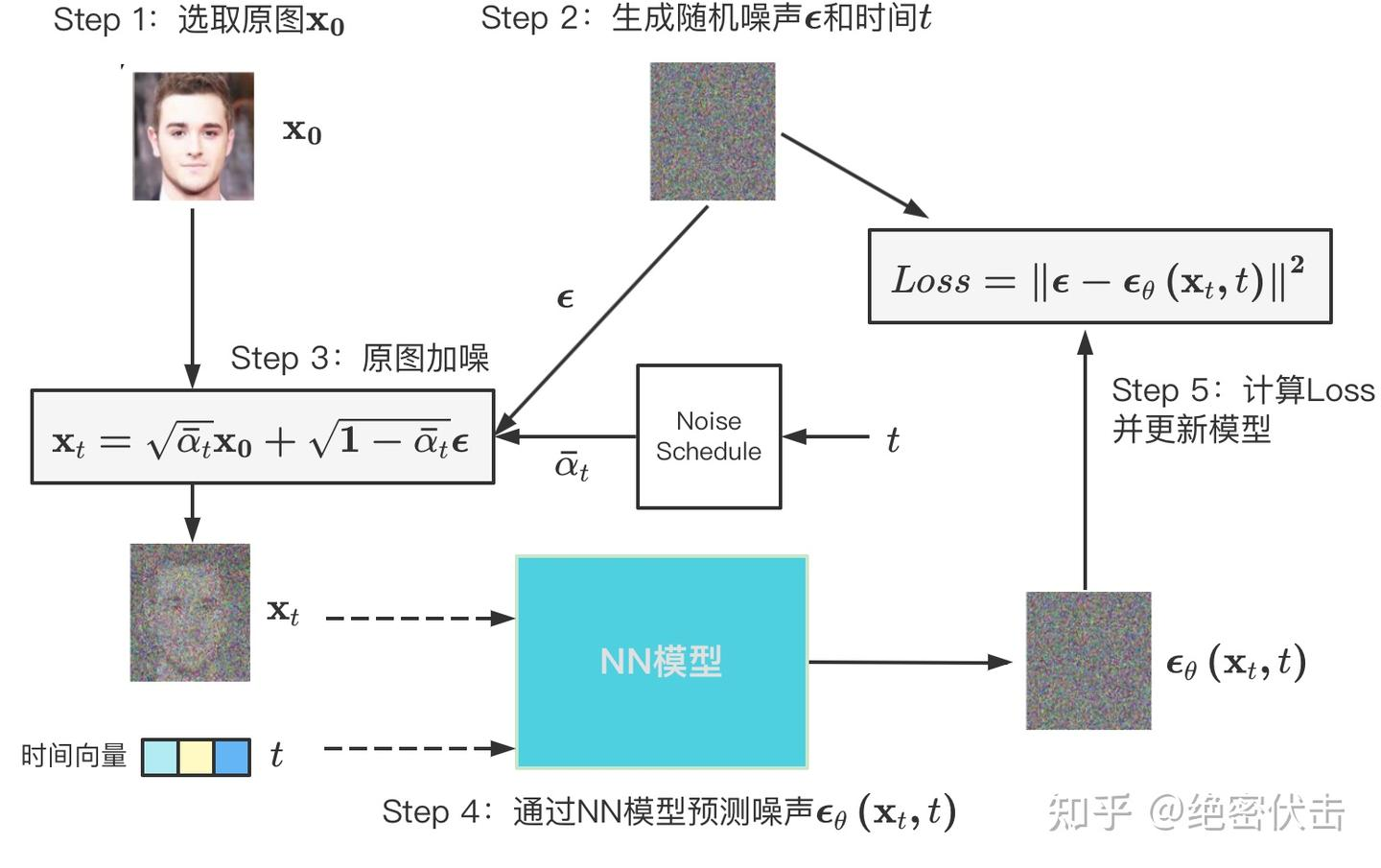
论文中的DDPM训练过程如下所示: 
从你的真实数据分布
:根据这个误差,计算损失函数关于模型参数 θ 的梯度,并使用梯度下降法(如 Adam 优化器)更新模型的权重,使得下次预测的噪声能更接近真实的噪声。 :计算真实噪声 和模型预测的噪声之间的均方误差 (Mean Squared Error, MSE)。 :构造出加噪后的图像 :将上一步生成的 和时间步 作为输入,送入我们的神经网络 计算出一个预测的噪声 until converged : 重复以上步骤,直到模型的性能不再提升(即收敛)。
DDPM如何生成图片
在得到预估噪声 
从一个标准正态分布(高斯分布)中随机采样一个样本
网上有很多DDPM的实现,包括论文中基于tensorflow的实现,还有基于pytorch的实现,但是由于代码结构复杂,很难上手。为了便于理解以及快速运行,我们将代码合并在一个文件里面,基于tf2.5实现,直接copy过去就能运行。代码主要分为3个部分:DDPM前向和反向过程(都在GaussianDiffusion一个类里面实现)、模型训练过程、新图片生成过程。
DDPM前向和后向过程代码如下:
import pandas as pd
import numpy as np
import os
import numpy as np
import sys
import pandas as pd
from numpy import arange
import math
import pyecharts
import sys,base64,urllib,re
import multiprocessing
from sklearn.metrics import roc_auc_score
from sklearn.metrics import ndcg_score
import warnings
from optparse import OptionParser
import logging
import logging.config
import time
import tensorflow as tf
from sklearn.preprocessing import normalize
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense, Dropout, Input
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import LeakyReLU, Conv2D
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import datasets
from tensorflow import keras
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# beta schedule
def linear_beta_schedule(timesteps):
scale = 1000 / timesteps
beta_start = scale * 0.0001
beta_end = scale * 0.02
return np.linspace(beta_start, beta_end, timesteps, dtype=np.float64)
def cosine_beta_schedule(timesteps, s=0.008):
"""
cosine schedule
as proposed in https://arxiv.org/abs/2102.09672
"""
steps = timesteps + 1
x = np.linspace(0, timesteps, steps, dtype=np.float64)
alphas_cumprod = np.cos(((x / timesteps) + s) / (1 + s) * math.pi * 0.5) ** 2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return np.clip(betas, 0, 0.999)
class GaussianDiffusion:
def __init__(
self,
timesteps=1000,
beta_schedule='linear'
):
self.timesteps = timesteps
#Calculate beta
if beta_schedule == 'linear':
betas = linear_beta_schedule(timesteps)
elif beta_schedule == 'cosine':
betas = cosine_beta_schedule(timesteps)
else:
raise ValueError(f'unknown beta schedule {beta_schedule}')
#Calculate alpha list, ᾱ_t cumulative product and ᾱ_{t-1} cumulative product
alphas = 1. - betas
alphas_cumprod = np.cumprod(alphas, axis=0)
alphas_cumprod_prev = np.append(1., alphas_cumprod[:-1])
self.betas = tf.constant(betas, dtype=tf.float32)
self.alphas_cumprod = tf.constant(alphas_cumprod, dtype=tf.float32)
self.alphas_cumprod_prev = tf.constant(alphas_cumprod_prev, dtype=tf.float32)
# calculations for diffusion q(x_t | x_{t-1}) and others
self.sqrt_alphas_cumprod = tf.constant(np.sqrt(self.alphas_cumprod), dtype=tf.float32)
self.sqrt_one_minus_alphas_cumprod = tf.constant(np.sqrt(1.0 - self.alphas_cumprod), dtype=tf.float32)
self.log_one_minus_alphas_cumprod = tf.constant(np.log(1. - alphas_cumprod), dtype=tf.float32)
self.sqrt_recip_alphas_cumprod = tf.constant(np.sqrt(1. / alphas_cumprod), dtype=tf.float32)
self.sqrt_recipm1_alphas_cumprod = tf.constant(np.sqrt(1. / alphas_cumprod - 1), dtype=tf.float32)
# calculations for posterior q(x_{t-1} | x_t, x_0)
self.posterior_variance = (
betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)
)
# below: log calculation clipped because the posterior variance is 0 at the beginning
# of the diffusion chain
self.posterior_log_variance_clipped = tf.constant(
np.log(np.maximum(self.posterior_variance, 1e-20)), dtype=tf.float32)
self.posterior_mean_coef1 = tf.constant(
betas * np.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod), dtype=tf.float32)
self.posterior_mean_coef2 = tf.constant(
(1. - alphas_cumprod_prev) * np.sqrt(alphas) / (1. - alphas_cumprod), dtype=tf.float32)
@staticmethod
def _extract(a, t, x_shape):
"""
Extract some coefficients at specified timesteps,
then reshape to [batch_size, 1, 1, 1, 1, ...] for broadcasting purposes.
"""
bs, = t.shape
assert x_shape[0] == bs
out = tf.gather(a, t)
assert out.shape == [bs]
return tf.reshape(out, [bs] + ((len(x_shape) - 1) * [1]))
# forward diffusion (using the nice property): q(x_t | x_0)
def q_sample(self, x_start, t, noise=None):
if noise is None:
noise = tf.random.normal(shape=x_start.shape)
sqrt_alphas_cumprod_t = self._extract(self.sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = self._extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# Get the mean and variance of q(x_t | x_0).
def q_mean_variance(self, x_start, t):
mean = self._extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
variance = self._extract(1.0 - self.alphas_cumprod, t, x_start.shape)
log_variance = self._extract(self.log_one_minus_alphas_cumprod, t, x_start.shape)
return mean, variance, log_variance
# Compute the mean and variance of the diffusion posterior: q(x_{t-1} | x_t, x_0)
def q_posterior_mean_variance(self, x_start, x_t, t):
posterior_mean = (
self._extract(self.posterior_mean_coef1, t, x_t.shape) * x_start
+ self._extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
)
posterior_variance = self._extract(self.posterior_variance, t, x_t.shape)
posterior_log_variance_clipped = self._extract(self.posterior_log_variance_clipped, t, x_t.shape)
return posterior_mean, posterior_variance, posterior_log_variance_clipped
# compute x_0 from x_t and pred noise: the reverse of `q_sample`
def predict_start_from_noise(self, x_t, t, noise):
return (
self._extract(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
self._extract(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
)
# compute predicted mean and variance of p(x_{t-1} | x_t)
def p_mean_variance(self, model, x_t, t, clip_denoised=True):
# predict noise using model
pred_noise = model([x_t, t])
# get the predicted x_0: different from the algorithm2 in the paper
x_recon = self.predict_start_from_noise(x_t, t, pred_noise)
if clip_denoised:
x_recon = tf.clip_by_value(x_recon, -1., 1.)
model_mean, posterior_variance, posterior_log_variance = \
self.q_posterior_mean_variance(x_recon, x_t, t)
return model_mean, posterior_variance, posterior_log_variance
def p_sample(self, model, x_t, t, clip_denoised=True):
# predict mean and variance
model_mean, _, model_log_variance = self.p_mean_variance(model, x_t, t,
clip_denoised=clip_denoised)
noise = tf.random.normal(shape=x_t.shape)
# no noise when t == 0
nonzero_mask = tf.reshape(1 - tf.cast(tf.equal(t, 0), tf.float32), [x_t.shape[0]] + [1] * (len(x_t.shape) - 1))
# compute x_{t-1}
pred_img = model_mean + nonzero_mask * tf.exp(0.5 * model_log_variance) * noise
return pred_img
def p_sample_loop(self, model, shape):
batch_size = shape[0]
# start from pure noise (for each example in the batch)
img = tf.random.normal(shape=shape)
imgs = []
for i in tqdm(reversed(range(0, self.timesteps)), desc='sampling loop time step', total=self.timesteps):
img = self.p_sample(model, img, tf.fill([batch_size], i))
imgs.append(img.numpy())
return imgs
def sample(self, model, image_size, batch_size=8, channels=3):
return self.p_sample_loop(model, shape=[batch_size, image_size, image_size, channels])
# compute train losses
def train_losses(self, model, x_start, t):
# generate random noise
noise = tf.random.normal(shape=x_start.shape)
# get x_t
x_noisy = self.q_sample(x_start, t, noise=noise)
model.train_on_batch([x_noisy, t], noise)
predicted_noise = model([x_noisy, t])
loss = model.loss(noise, predicted_noise)
return loss
# Load the dataset
def load_data():
(x_train, y_train), (_, _) = mnist.load_data()
x_train = (x_train.astype(np.float32) - 127.5)/127.5
return (x_train, y_train)
print("forward diffusion: q(x_t | x_0)")
timesteps = 500
X_train, y_train = load_data()
gaussian_diffusion = GaussianDiffusion(timesteps)
plt.figure(figsize=(16, 8))
x_start = X_train[7:8]
for idx, t in enumerate([0, 50, 100, 200, 499]):
x_noisy = gaussian_diffusion.q_sample(x_start, t=tf.convert_to_tensor([t]))
x_noisy = x_noisy.numpy()
x_noisy = x_noisy.reshape(28, 28)
plt.subplot(1, 5, 1 + idx)
plt.imshow(x_noisy, cmap="gray")
plt.axis("off")
plt.title(f"t={t}")运行上面代码,我们可以得到前向过程的效果如下图所示: 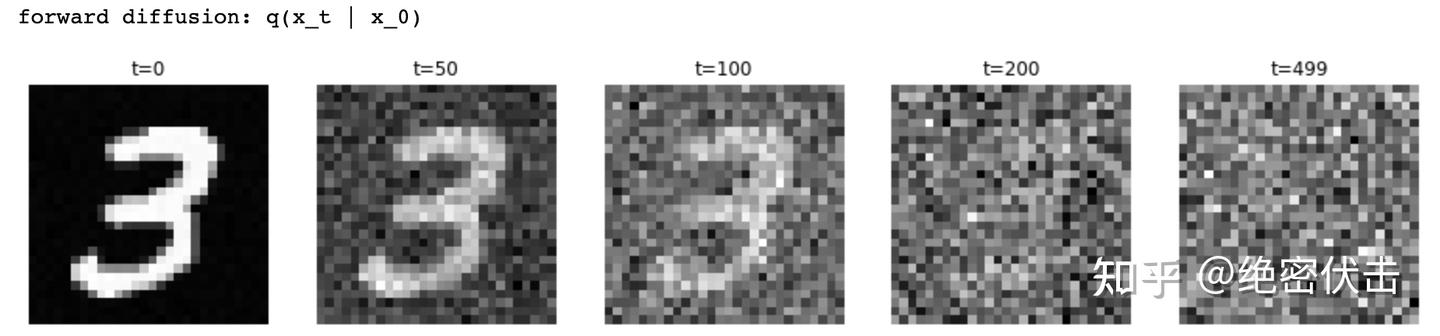 从图中可以看出,随着不断加噪,图片变得越来越模糊,最后变成随机噪声。 接下来是模型训练过程,我们先使用一个简单的残差网络模型,代码如下:
从图中可以看出,随着不断加噪,图片变得越来越模糊,最后变成随机噪声。 接下来是模型训练过程,我们先使用一个简单的残差网络模型,代码如下:
# ResNet model
class ResNet(keras.layers.Layer):
def __init__(self, in_channels, out_channels, name='ResNet', **kwargs):
super(ResNet, self).__init__(name=name, **kwargs)
self.in_channels = in_channels
self.out_channels = out_channels
def get_config(self):
config = super(ResNet, self).get_config()
config.update({'in_channels': self.in_channels, 'out_channels': self.out_channels})
return config
@classmethod
def from_config(cls, config, custom_objects=None):
return cls(**config)
def build(self, input_shape):
self.conv1 = Sequential([
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=3, padding='same')
])
self.conv2 = Sequential([
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=3, padding='same', name='conv2')
])
def call(self, inputs_all, dropout=None, **kwargs):
"""
`x` has shape `[batch_size, height, width, in_dim]`
"""
x, t = inputs_all
h = self.conv1(x)
h = self.conv2(h)
h += x
return h
def build_DDPM(nn_model):
nn_model.trainablea = True
inputs = Input(shape=(28, 28, 1,))
timesteps=Input(shape=(1,))
outputs = nn_model([inputs, timesteps])
ddpm = Model(inputs=[inputs, timesteps], outputs=outputs)
ddpm.compile(loss=keras.losses.mse, optimizer=Adam(5e-4))
return ddpm
# train ddpm
def train_ddpm(ddpm, gaussian_diffusion, epochs=1, batch_size=128, timesteps=500):
#Loading the data
X_train, y_train = load_data()
step_cont = len(y_train) // batch_size
step = 1
for i in range(1, epochs + 1):
for s in range(step_cont):
if (s+1)*batch_size > len(y_train):
break
images = X_train[s*batch_size:(s+1)*batch_size]
images = tf.reshape(images, [-1, 28, 28 ,1])
t = tf.random.uniform(shape=[batch_size], minval=0, maxval=timesteps, dtype=tf.int32)
loss = gaussian_diffusion.train_losses(ddpm, images, t)
if step == 1 or step % 100 == 0:
print("[step=%s]\tloss: %s" %(step, str(tf.reduce_mean(loss).numpy())))
step += 1
print("[ResNet] train ddpm")
nn_model = ResNet(in_channels=1, out_channels=1)
ddpm = build_DDPM(nn_model)
gaussian_diffusion = GaussianDiffusion(timesteps=500)
train_ddpm(ddpm, gaussian_diffusion, epochs=10, batch_size=64, timesteps=500)
print("[ResNet] generate new images")
generated_images = gaussian_diffusion.sample(ddpm, 28, batch_size=64, channels=1)
fig = plt.figure(figsize=(12, 12), constrained_layout=True)
gs = fig.add_gridspec(8, 8)
imgs = generated_images[-1].reshape(8, 8, 28, 28)
for n_row in range(8):
for n_col in range(8):
f_ax = fig.add_subplot(gs[n_row, n_col])
f_ax.imshow((imgs[n_row, n_col]+1.0) * 255 / 2, cmap="gray")
f_ax.axis("off")
print("[ResNet] show the denoise steps")
fig = plt.figure(figsize=(12, 12), constrained_layout=True)
gs = fig.add_gridspec(16, 16)
for n_row in range(16):
for n_col in range(16):
f_ax = fig.add_subplot(gs[n_row, n_col])
t_idx = (timesteps // 16) * n_col if n_col < 15 else -1
img = generated_images[t_idx][n_row].reshape(28, 28)
f_ax.imshow((img+1.0) * 255 / 2, cmap="gray")
f_ax.axis("off")运行上面代码,我们能得到训练Loss如下:  训练完后生成的图片如下图所示:
训练完后生成的图片如下图所示:  可以看到效果非常差,基本看不出是手写数字 实际应用中一般是基于U-Net模型,模型结构如下:
可以看到效果非常差,基本看不出是手写数字 实际应用中一般是基于U-Net模型,模型结构如下: 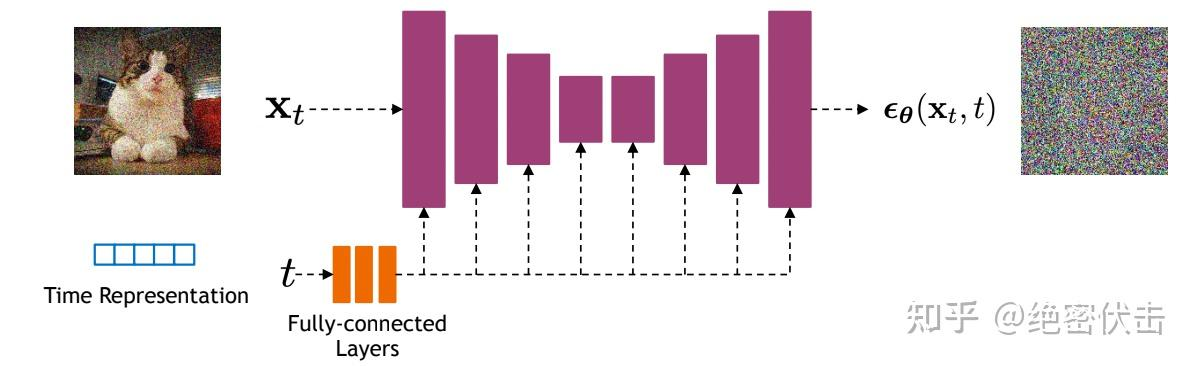 使用U-Net进行训练的代码如下:
使用U-Net进行训练的代码如下:
"""
U-Net model
as proposed in https://arxiv.org/pdf/1505.04597v1.pdf
"""
# use sinusoidal position embedding to encode time step (https://arxiv.org/abs/1706.03762)
def timestep_embedding(timesteps, dim, max_period=10000):
"""
Create sinusoidal timestep embeddings.
:param timesteps: a 1-D Tensor of N indices, one per batch element.
These may be fractional.
:param dim: the dimension of the output.
:param max_period: controls the minimum frequency of the embeddings.
:return: an [N x dim] Tensor of positional embeddings.
"""
half = dim // 2
freqs = tf.exp(
-math.log(max_period) * tf.experimental.numpy.arange(start=0, stop=half, step=1, dtype=tf.float32) / half
)
args = timesteps[:, ] * freqs
embedding = tf.concat([tf.cos(args), tf.sin(args)], axis=-1)
if dim % 2:
embedding = tf.concat([embedding, tf.zeros_like(embedding[:, :1])], axis=-1)
return embedding
# upsample
class Upsample(keras.layers.Layer):
def __init__(self, channels, use_conv=False, name='Upsample', **kwargs):
super(Upsample, self).__init__(name=name, **kwargs)
self.use_conv = use_conv
self.channels = channels
def get_config(self):
config = super(Upsample, self).get_config()
config.update({'channels': self.channels, 'use_conv': self.use_conv})
return config
@classmethod
def from_config(cls, config, custom_objects=None):
return cls(**config)
def build(self, input_shape):
if self.use_conv:
self.conv = keras.layers.Conv2D(filters=self.channels, kernel_size=3, padding='same')
def call(self, inputs_all, dropout=None, **kwargs):
x, t = inputs_all
x = tf.image.resize_with_pad(x, target_height=x.shape[1]*2, target_width=x.shape[2]*2, method='nearest')
# if self.use_conv:
# x = self.conv(x)
return x
# downsample
class Downsample(keras.layers.Layer):
def __init__(self, channels, use_conv=True, name='Downsample', **kwargs):
super(Downsample, self).__init__(name=name, **kwargs)
self.use_conv = use_conv
self.channels = channels
def get_config(self):
config = super(Downsample, self).get_config()
config.update({'channels': self.channels, 'use_conv': self.use_conv})
return config
@classmethod
def from_config(cls, config, custom_objects=None):
return cls(**config)
def build(self, input_shape):
if self.use_conv:
self.op = keras.layers.Conv2D(filters=self.channels, kernel_size=3, strides=2, padding='same')
else:
self.op = keras.layers.AveragePooling2D(strides=(2, 2))
def call(self, inputs_all, dropout=None, **kwargs):
x, t = inputs_all
return self.op(x)
# Residual block
class ResidualBlock(keras.layers.Layer):
def __init__(
self,
in_channels,
out_channels,
time_channels,
use_time_emb=True,
name='residul_block', **kwargs
):
super(ResidualBlock, self).__init__(name=name, **kwargs)
self.in_channels = in_channels
self.out_channels = out_channels
self.time_channels = time_channels
self.use_time_emb = use_time_emb
def get_config(self):
config = super(ResidualBlock, self).get_config()
config.update({
'time_channels': self.time_channels,
'in_channels': self.in_channels,
'out_channels': self.out_channels,
'use_time_emb': self.use_time_emb
})
return config
@classmethod
def from_config(cls, config, custom_objects=None):
return cls(**config)
def build(self, input_shape):
self.dense_ = keras.layers.Dense(units=self.out_channels, activation=None)
self.dense_short = keras.layers.Dense(units=self.out_channels, activation=None)
self.conv1 = [
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=3, padding='same')
]
self.conv2 = [
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=3, padding='same', name='conv2')
]
self.conv3 = [
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=1, name='conv3')
]
self.activate = keras.layers.LeakyReLU()
def call(self, inputs_all, dropout=None, **kwargs):
"""
`x` has shape `[batch_size, height, width, in_dim]`
`t` has shape `[batch_size, time_dim]`
"""
x, t = inputs_all
h = x
for module in self.conv1:
h = module(x)
# Add time step embeddings
if self.use_time_emb:
time_emb = self.dense_(self.activate(t))[:, None, None, :]
h += time_emb
for module in self.conv2:
h = module(h)
if self.in_channels != self.out_channels:
for module in self.conv3:
x = module(x)
return h + x
else:
return h + x
# Attention block with shortcut
class AttentionBlock(keras.layers.Layer):
def __init__(self, channels, num_heads=1, name='attention_block', **kwargs):
super(AttentionBlock, self).__init__(name=name, **kwargs)
self.channels = channels
self.num_heads = num_heads
self.dense_layers = []
def get_config(self):
config = super(AttentionBlock, self).get_config()
config.update({'channels': self.channels, 'num_heads': self.num_heads})
return config
@classmethod
def from_config(cls, config, custom_objects=None):
return cls(**config)
def build(self, input_shape):
for i in range(3):
dense_ = keras.layers.Conv2D(filters=self.channels, kernel_size=1)
self.dense_layers.append(dense_)
self.proj = keras.layers.Conv2D(filters=self.channels, kernel_size=1)
def call(self, inputs_all, dropout=None, **kwargs):
inputs, t = inputs_all
H = inputs.shape[1]
W = inputs.shape[2]
C = inputs.shape[3]
qkv = inputs
q = self.dense_layers[0](qkv)
k = self.dense_layers[1](qkv)
v = self.dense_layers[2](qkv)
attn = tf.einsum("bhwc,bHWc->bhwHW", q, k)* (int(C) ** (-0.5))
attn = tf.reshape(attn, [-1, H, W, H * W])
attn = tf.nn.softmax(attn, axis=-1)
attn = tf.reshape(attn, [-1, H, W, H, W])
h = tf.einsum('bhwHW,bHWc->bhwc', attn, v)
h = self.proj(h)
return h + inputs
# upsample
class UNetModel(keras.layers.Layer):
def __init__(
self,
in_channels=3,
model_channels=128,
out_channels=3,
num_res_blocks=2,
attention_resolutions=(8, 16),
dropout=0,
channel_mult=(1, 2, 2, 2),
conv_resample=True,
num_heads=4,
name='UNetModel',
**kwargs
):
super(UNetModel, self).__init__(name=name, **kwargs)
self.in_channels = in_channels
self.model_channels = model_channels
self.out_channels = out_channels
self.num_res_blocks = num_res_blocks
self.attention_resolutions = attention_resolutions
self.dropout = dropout
self.channel_mult = channel_mult
self.conv_resample = conv_resample
self.num_heads = num_heads
self.time_embed_dim = self.model_channels * 4
def build(self, input_shape):
# time embedding
self.time_embed = [
keras.layers.Dense(self.time_embed_dim, activation=None),
keras.layers.LeakyReLU(),
keras.layers.Dense(self.time_embed_dim, activation=None)
]
# down blocks
self.conv = keras.layers.Conv2D(filters=self.model_channels, kernel_size=3, padding='same')
self.down_blocks = []
down_block_chans = [self.model_channels]
ch = self.model_channels
ds = 1
index = 0
for level, mult in enumerate(self.channel_mult):
for _ in range(self.num_res_blocks):
layers = [
ResidualBlock(
in_channels=ch,
out_channels=mult * self.model_channels,
time_channels=self.time_embed_dim,
name='resnet_'+str(index)
)
]
index += 1
ch = mult * self.model_channels
if ds in self.attention_resolutions:
layers.append(AttentionBlock(ch, num_heads=self.num_heads))
self.down_blocks.append(layers)
down_block_chans.append(ch)
if level != len(self.channel_mult) - 1: # don't use downsample for the last stage
self.down_blocks.append(Downsample(ch, self.conv_resample))
down_block_chans.append(ch)
ds *= 2
# middle block
self.middle_block = [
ResidualBlock(ch, ch, self.time_embed_dim, name='res1'),
AttentionBlock(ch, num_heads=self.num_heads),
ResidualBlock(ch, ch, self.time_embed_dim, name='res2')
]
# up blocks
self.up_blocks = []
index = 0
for level, mult in list(enumerate(self.channel_mult))[::-1]:
for i in range(self.num_res_blocks + 1):
layers = []
layers.append(
ResidualBlock(
in_channels=ch + down_block_chans.pop(),
out_channels=self.model_channels * mult,
time_channels=self.time_embed_dim,
name='up_resnet_'+str(index)
)
)
layer_num = 1
ch = self.model_channels * mult
if ds in self.attention_resolutions:
layers.append(AttentionBlock(ch, num_heads=self.num_heads))
if level and i == self.num_res_blocks:
layers.append(Upsample(ch, self.conv_resample))
ds //= 2
self.up_blocks.append(layers)
index += 1
self.out = Sequential([
keras.layers.LeakyReLU(),
keras.layers.Conv2D(filters=self.out_channels, kernel_size=3, padding='same')
])
def call(self, inputs, dropout=None, **kwargs):
"""
Apply the model to an input batch.
:param x: an [N x H x W x C] Tensor of inputs. N, H, W, C
:param timesteps: a 1-D batch of timesteps.
:return: an [N x C x ...] Tensor of outputs.
"""
x, timesteps = inputs
hs = []
# time step embedding
emb = timestep_embedding(timesteps, self.model_channels)
for module in self.time_embed:
emb = module(emb)
# down stage
h = x
h = self.conv(h)
hs = [h]
for module_list in self.down_blocks:
if isinstance(module_list, list):
for module in module_list:
h = module([h, emb])
else:
h = module_list([h, emb])
hs.append(h)
# middle stage
for module in self.middle_block:
h = module([h, emb])
# up stage
for module_list in self.up_blocks:
cat_in = tf.concat([h, hs.pop()], axis=-1)
h = cat_in
for module in module_list:
h = module([h, emb])
return self.out(h)
print("[U-Net] train ddpm")
nn_model = UNetModel(
in_channels=1,
model_channels=96,
out_channels=1,
channel_mult=(1, 2, 2),
attention_resolutions=[]
)
ddpm = build_DDPM(nn_model)
gaussian_diffusion = GaussianDiffusion(timesteps=500)
train_ddpm(ddpm, gaussian_diffusion, epochs=10, batch_size=64, timesteps=500)
print("[U-Net] generate new images")
generated_images = gaussian_diffusion.sample(ddpm, 28, batch_size=64, channels=1)
fig = plt.figure(figsize=(12, 12), constrained_layout=True)
gs = fig.add_gridspec(8, 8)
imgs = generated_images[-1].reshape(8, 8, 28, 28)
for n_row in range(8):
for n_col in range(8):
f_ax = fig.add_subplot(gs[n_row, n_col])
f_ax.imshow((imgs[n_row, n_col]+1.0) * 255 / 2, cmap="gray")
f_ax.axis("off")
print("[U-Net] show the denoise steps")
fig = plt.figure(figsize=(12, 12), constrained_layout=True)
gs = fig.add_gridspec(16, 16)
for n_row in range(16):
for n_col in range(16):
f_ax = fig.add_subplot(gs[n_row, n_col])
t_idx = (timesteps // 16) * n_col if n_col < 15 else -1
img = generated_images[t_idx][n_row].reshape(28, 28)
f_ax.imshow((img+1.0) * 255 / 2, cmap="gray")
f_ax.axis("off")运行上面代码,训练Loss如下:  训练好后生成的图片如下:
训练好后生成的图片如下:  可以看到明显好于前面基于ResNet实现的效果,而整个反向过程(去噪过程)的效果如下图所示。
可以看到明显好于前面基于ResNet实现的效果,而整个反向过程(去噪过程)的效果如下图所示。 