全连接神经网络（Full Connect Neural Network）
全连接神经网络原理
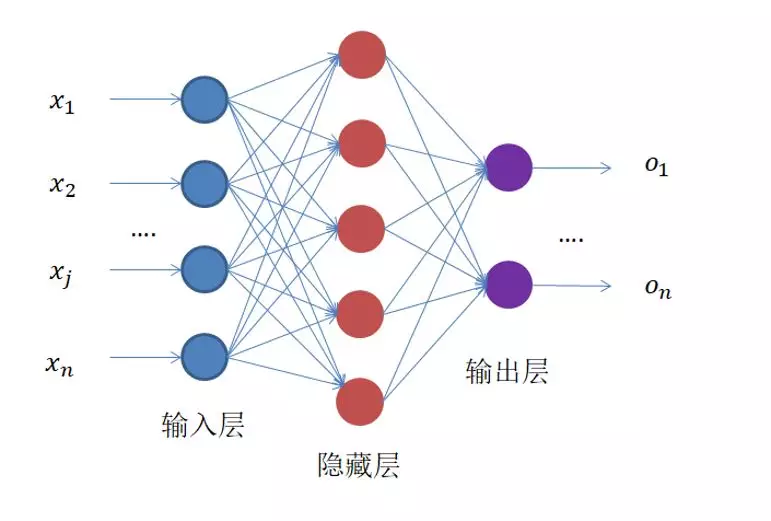
就是这么一个东西，左边输入，中间计算，右边输出。
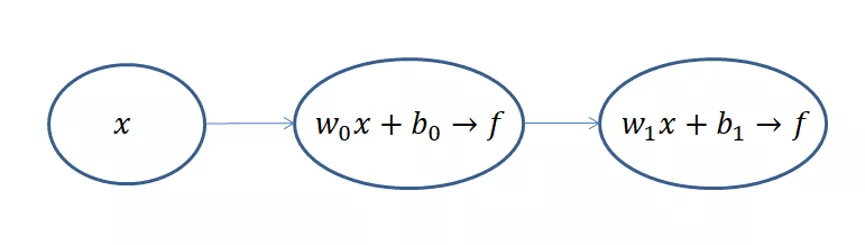
不算输入层，上面的网络结构总共有两层，隐藏层和输出层，它们“圆圈”里的计算都是公式(4.1)和(4.2)的计算组合：
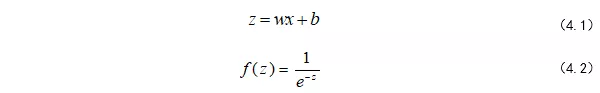
每一级都是利用前一级的输出做输入，再经过圆圈内的组合计算，输出到下一级。 看到这里，可能很多人会疑惑，为什么要加上f(z)这个运算，这个运算的目的是为了将输出的值域压缩到（0，1），也就是所谓的归一化，因为每一级输出的值都将作为下一级的输入，只有将输入归一化了，才会避免某个输入无穷大，导致其他输入无效，最终网络训练效果非常不好。 为了解决这个问题设计了，一个反向传播算法，反向传播的过程：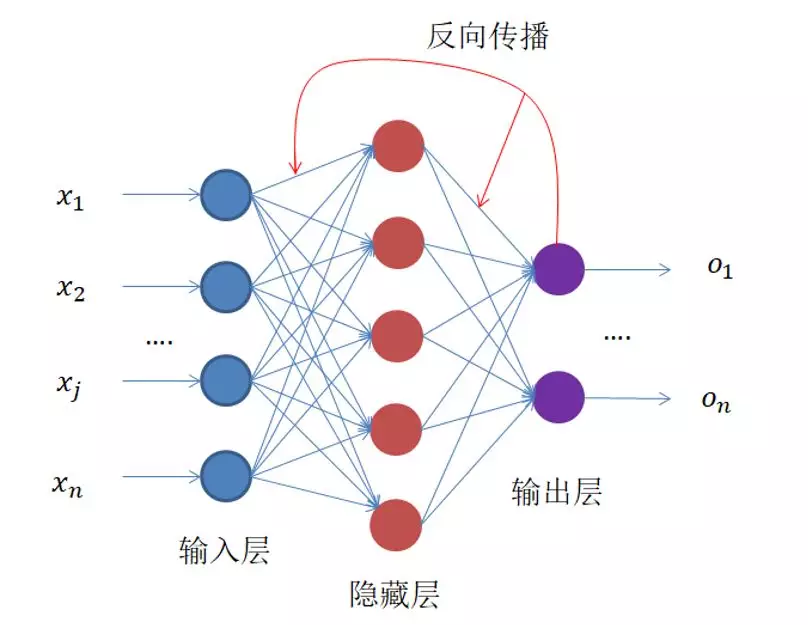
- 前向传播 (Forward Propagation): 将训练数据输入网络，从输入层开始，逐层计算，直到输出层得到预测结果。
- 反向传播 (Backward Propagation): 计算误差: 将网络的预测结果与真实标签进行比较，计算出损失函数的值。
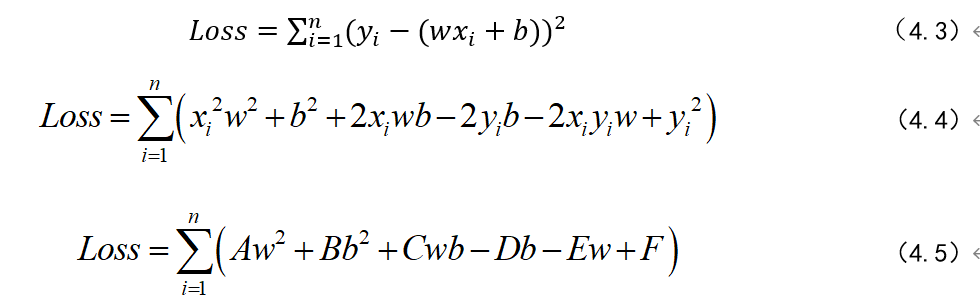公式经过化简，我们可以看到A、B、C、D、E、F都是常系数，未知数就是w 和b ，也就是为了让Loss 最小，我们要求解出最佳的w 和b 。这时我们稍微想象一下，如果这是个二维空间，那么我们相当于要找一条曲线，让它与坐标轴上所有样本点距离最小。如下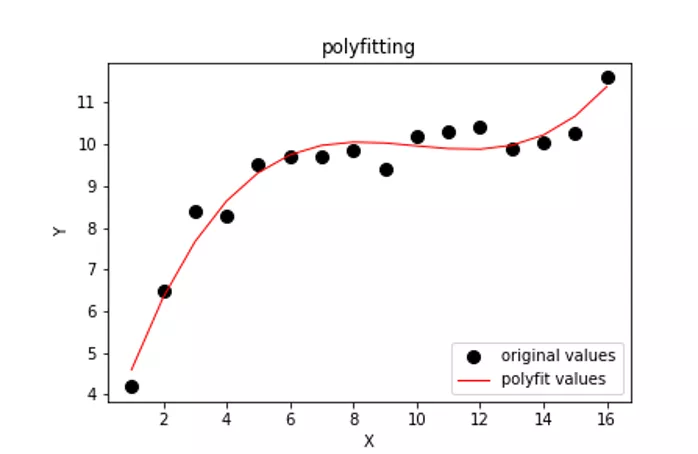
我们可以将Loss 方程转化为一个三维图像求最优解的过程。三维图像就像一个“碗”，如下图所示，它和二维空间的抛物线一样，存在极值，那我们只要将极值求出，那就保证了我们能求出最优的（w , b）也就是这个“碗底”的坐标，使Loss 最小。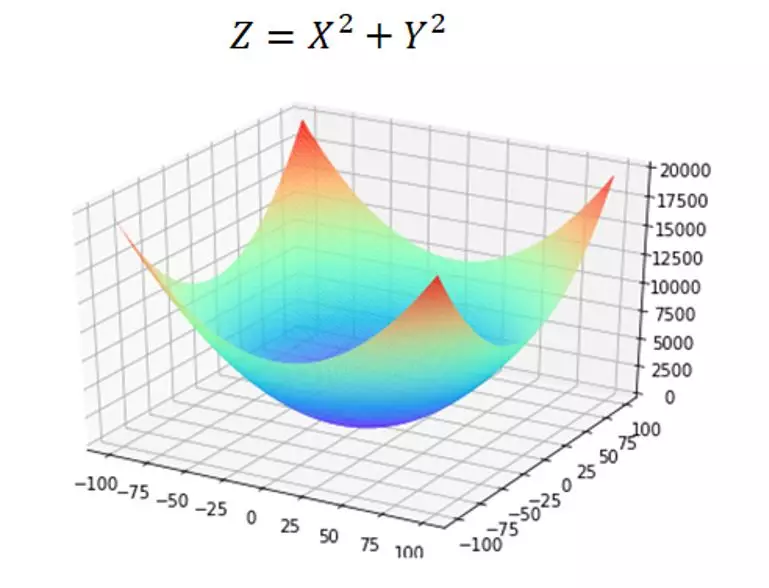
当我们列完函数方程之后，做的第一件事就是对这个函数求偏导，也就是对X，Y分别求导，在求导过程中，把其他的未知量当成常数即可。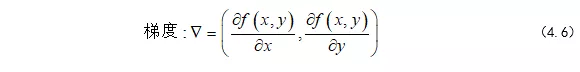 
我们每移动一步，坐标就会更新：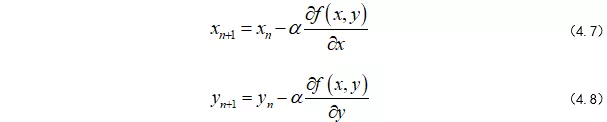 
当然，这是三维空间中的，假如我们在多维空间漫步呢，其实也是一样的，也就是对各个维度求偏导，更新自己的坐标。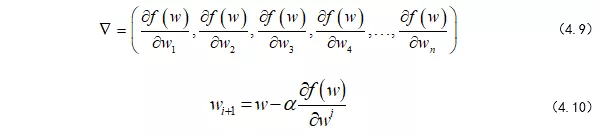 
其中，w的上标 i 表示第几个w，下标n表示第几步，α是学习率，后面会介绍α的作用。所以，我们可以将整个求解过程看做下山（求偏导过程），为此，我们先初始化自己的初始位置。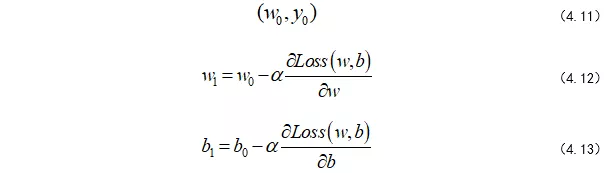 
迭代：使用计算出的梯度来更新网络中的权重和偏置，通常会结合梯度下降等优化算法。 更新的目的是让网络在下一次前向传播中做出更准确的预测。
我们将整个求解过程称为梯度下降求解法。
这里还需要补充的是为什么要有学习率α，通常来说，学习率是可以随意设置，你可以根据过去的经验或书本资料选择一个最佳值，或凭直觉估计一个合适值，一般在（0，1）之间。这样做可行，但并非永远可行。事实上选择学习率是一件比较困难的事，下图显示了应用不同学习率后出现的各类情况，其中epoch为使用训练集全部样本训练一次的单位，loss表示损失。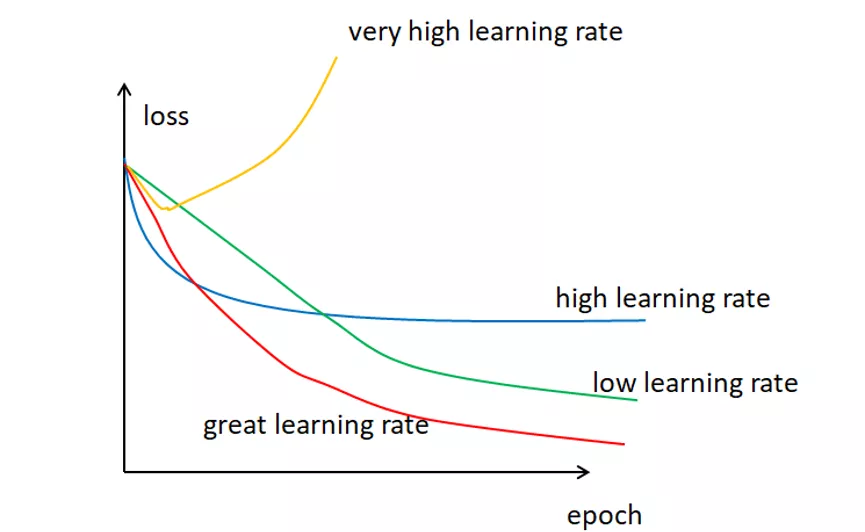 
可以发现，学习率直接影响我们的模型能够以多快的速度收敛到局部最小值（也就是达到最好的精度）。一般来说，学习率越大，神经网络学习速度越快。如果学习率太小，网络很可能会陷入局部最优；但是如果太大，超过了极值，损失就会停止下降，在某一位置反复震荡。
也就是说，如果我们选择了一个合适的学习率，我们不仅可以在更短的时间内训练好模型，还可以节省各种运算资源的花费。
如何选择？业界并没有特别硬性的定论，总的来说就是试出来的，看哪个学习率能让Loss收敛得更快，Loss最小，就选哪个。